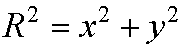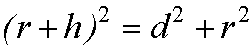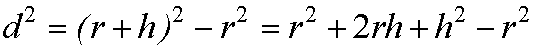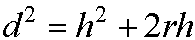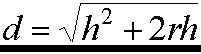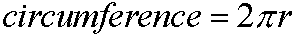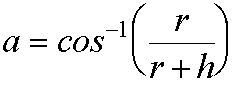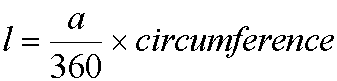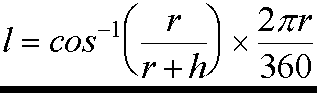Calculating the Distance to the Horizon

For Any Game

ASSUMPTIONS

This is all based on the assumption that the horizon is the point on the world's surface at which the line of sight of the viewer, whatever their height, becomes parallel (tangential) to the surface of the world, and meets the surface of the world (so that the viewer cannot see any further than it). It also assumes a perfectly spherical world, and does not take into account any effects on the visible horizon due to terrain or atmospheric refraction.

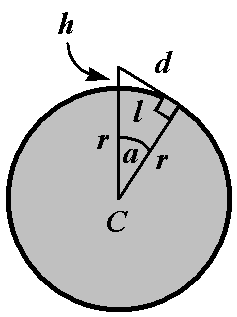
The diagram below shows this:

The geometry of the situation

Where:

The grey circle is the planet in question.
C is the centre of the planet.
r is the radius of the planet.
h is the height of the observer's eyes (or camera, or whatever) above the surface of the planet.
d is the distance from the observer's eyes to the horizon.
l is the distance from the observer to the horizon along the curve of the planet.
a is the angle between the observer and the horizon, measured from the centre of the planet.

The triangle is a right-angled one, whose sides are the radius of the planet (r), the radius of the planet plus the height of the observer (r + h), and the distance to the horizon (d).

Note that I do not mention units in any of the equations on this page. This is entirely deliberate. As long as the same units are used consistently throughout, these equations should work for any measurement system .

METHOD 1

Assumptions | Method 2

For a right-angled triangle:

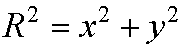
Where:

R is the longest side (the hypotenuse),

x and y are the other two sides.

Using this equation on the triangle in the figure above, the longest side is the radius of the planet plus the height of the observer (r + h), and the other two sides are d and r. So:

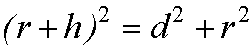
Or, re-arranged:

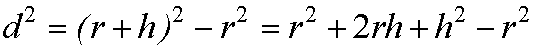
Or:

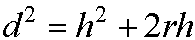
So the total distance to the horizon is given by:

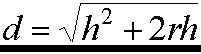
This equation will work for any size world, and any height of observer. Anyone using this equation should be aware, however, that its result, d, is the straight-line distance from the observer's eyes to the horizon, and not the distance to the horizon along the ground (which will be longer). However, it should be a good enough approximation for cases where h is much less than r, which is certainly going to be the case on any natural terrain feature on a solid planet.

METHOD 2

Assumptions | Method 1

For cases where the approximation, d, is not sufficient, a more accurate distance, l, can be calculated (though this still makes the assumption that the planet is spherical). First, the circumference of the planet is calculated, as:

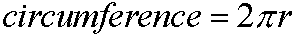
Secondly, the angle a, the angle in degrees between the observer and the horizon, measured from the centre of the planet, should be calculated. This is given by:

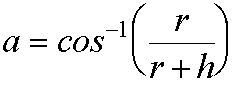
From these two values, the distance l can be calculated as the proportion of the circumference of the planet which the angle a covers. This is obtained from the equation:

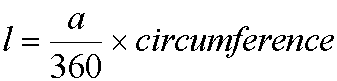
Or:

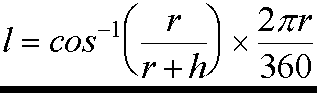
Note that the angle output by the cos^-1 function should be in degrees, otherwise this equation will not work properly. If the output of the cos^-1 function is in radians simply multiply that by r alone to get the correct result.

This equation should also work for any size world, and will be more accurate than the one above, if a little more complicated.

Assumptions | Method 1 | Method 2

Send any comments to me at tony {dot} website {at} clockworksky {dot} net.

Back to My Roleplaying Page.

More on the calculation of the distance to the horizon can also be found at SailingIssues.Com and HowStuffWorks.